Matemáticas Fundamentación Teórica (basado en Resolución Gráfica de Problemas)

Índice de Contenido.
El comienzo: Singapore Math
Principios Básicos
Matemáticas en Infantil
- Conceptos básicos: cantidad, mayor que, menor que, igual, más, menos, anterior, posterior, comparar, ordenar.
Simetrías. - Series y Patrones.
- Pesas.
- Proporcionalidad.
- Comparación
- Ordenación
- Descomposición de Números y uso del complementos del 10.
- Bonds Numbers o Números enlazados.
- Uso de Regletas.
- Problemas gráficos y reales.
- Inicio al lenguaje matemático.
- Lectoescritura de números.
- Lúdico, uso de juegos matemáticos.
Primaria
- Cálculo
- Propiedades numéricas: conmutativa, asociativa, distributiva…
- Conceptos numéricos: dobles, triples, mitad, más, menos, más que, menos que, igual.
- Problemas gráficos y reales.
- Atención a la Diversidad.
- Representación de Números
- Sistema Métrico
- Longitud
- Superficie
- y sobre todo Resolución Gráfica de Problemas
- Problemas Gráficos y reales
- Ejemplos Resolución de Problemas
- Elementos que componen la Resolución de Problemas
Datos
Representación Gráfica
Cálculo
Prueba - ¿Cómo resolver un problema?
- Tipos de problemas
Cambio
Combinación
Comparación
Igualación
Multiplicación
División - Problemas Complejos
Fracciones
Tantos por cientos
Ángulos
Sistema métrico
Dinero
Tiempo
Con varias operaciones. - Evaluación
- Creación de Problemas
- Tratamiento de la información
- Uso del lenguaje matemático
- Herramientas de autor
- Documentos para trabajar
Nuestra Comunidad
Conclusiones
Agradecimientos
El comienzo
Punto de partida.
Tras la inquietud de parte del profesorado del CEIP Cristóbal Luque Onieva, de Priego de Córdoba, se comienza a investigar y se pretende mejorar las matemáticas del centro.

Comenzamos a trabajar con «Algoritmo ABN» y «Método Singapur» , método utilizado en Singapur en matemáticas. Este país copa los primeros puestos en el informe de rendimiento escolar (informe PISA).
Resumiendo nuestra metodología ecléctica: se basa en la resolución gráficas de problemas. Por tanto intenta evitar la abstracción y centrarse en lo concreto. Desde el concepto de número que se intenta ser manipulable a la resolución gráfica de problemas, el alumnado puede tocar y ver las matemáticas. Esto hace que sea más accesible al alumnado. Por eso también se adapta mejor a todos los niveles, incluso para alumnado de necesidades específicas de apoyo educativo, y por tanto atendiendo a la diversidad. También el concepto de número, hacerlo concreto y dejar la abstracción para cursos superiores.

Tras conocer este método se trabajó el curso 2012-2013 con el Alumnado de Apoyo a la integración, y 5º de E. Primaria. Ofreciendo buenos resultados.
También nos hemos formado con otros métodos, entre ellos «Algoritmo ABN«, donde vemos cosas positivas, sobre todo cómo aborda el tema del cálculo. Y entendemos que ABN, podría aportar cosas positivas de forma complementaria.
Así presentamos el trabajo de investigación mostrando un método ecléctico; basado en la resolución de problemas.
Principios Básicos
Se pueden establecer algunos principios básicos:
- Se basa en la solución de problemas.
- Se basa en lo concreto, todo se puede observar y tocar.
- Divertido y lúdico.
- Desde infantil, hasta cualquier etapa.
- Se puede iniciar desde cualquier curso, nivel o etapa.
- Favorece el cálculo mental.
- Mejora el razonamiento lógico matemático.
- Es el inicio al lenguaje matemático.
- Matemáticas más naturales y más concretas.
- Atiende a la Diversidad.
Matemáticas en Infantil
Conceptos básicos.
Desde infantil se trabaja el concepto de número, concreto y proporcional. Se usan tanto regletas Cuisenaire o cualquier elemento que pueda representar una cantidad. Pero mostrando no sólo la cantidad, sino la relación entre números. Así se pueden presentar problemas gráficos donde aparezca el concepto de número, concepto adicción y diferencia. Si es posible en forma de juego o de reto.

La gran diferencia de otros métodos es la misma proporcionalidad, no sólo la cantidad, que facilita la adquisición de conceptos básicos matemáticos como «mayor que«, «menor que«, «igual«, «más«, «menos«. Todo el trabajo se debe realizar de forma manipulativa, como series, patrones, descomposición, comparación.
Simetrías
Las Simetrías son una forma lúdica de juego, y se utiliza para a asimilación de concepto número, suma y diferencia, cantidad proporcionalidad, por tanto hace que se desarrolle el cálculo de forma lúdica. También se establecen claves para el uso de referencias espaciales y es el primer sistema de ecuaciones. Donde una parte debe ser igual a la otra. Se pueden realizar diferentes ejercicios dependiendo de dificultad.

Series y Patrones
Las Series y Patrones son otra forma de razonamiento y lógica. Las series se utilizan para el desarrollo de lógica, y trabajan los incrementos o decrementos de una cantidad, base de la multiplicación, división, permanencias de los objetos. Se pueden presentar series ascendentes desde una cantidad hasta otra, o series descendentes. Se irá secuenciando el nivel de dificultad.
+1 +2 +3 -1 -2 -3
+10 +20 +30 -10 -20 -30
Como anécdota decir que con un alumno trabajando «mayor que» y «menor que» al plantear una pregunta si había números menores que el 0, uno levantó la mano y dijo que el «-1», así se presentó la serie numérica del 10 al -10 y estuvo representándola con regletas. La serie la construyó él. Por tanto empezó a experimentar con números negativos. Y se nos planteó una pregunta, ¿se puede trabajar números enteros en 1º? A partir de ahí cuando se presentan series a este alumno descendentes o ascendentes se adapta la ficha con series que lleguen a los números negativos. Y sólo se ha trabajado esta serie. No ha habido la mayor explicación, lo ha interiorizado y experimentado.
Algunas actividades para realizar en papel:
Pesas
Proporcionalidad
Trabajamos las comparaciones, iniciamos las primeras preguntas. «¿Quién es mayor?», «¿y menor?«, «¿cómo son?«,…
Comparación
Al comparar dos elementos o números se aprecia el valor relativo, si es mayor, menor, igual y cuantos se diferencia. Inicio para los problemas de comparación e igualación. También da sentido a los signos de >, < y =.
 Ordenación
Ordenación
También la ordenación de números. Como hemos mencionado antes la series, se hacen visibles y manipulables. Se pueden ordenar de menor a mayor, de mayor a menor. Se puede analizar cuanta diferencia hay entre ellos y si es constante.

Descomposición de Números
Como ejercicios se utilizan las descomposición de números. Esto favorecerá el cálculo mental y el uso de propiedades numéricas, cálculo, lenguaje matemático. Esto es el inicio a los primeros problemas. Ejemplo: 10 = 3+6+1 5=2+3. Esto favorecerá el cálculo mental y interiorizar propiedades numéricas como la conmutativa, distributiva. También con la descomposición de números se muestra que un problema puede tener más de una solución matemática.
Complementos del 10, básicos para el cálculo mental y entender el sistema decimal.

Inicio del lenguaje matemático
10 = 3+6+1
10=2+8
Para el cálculo se realizan agrupaciones de 10 y por tanto hay que trabajar los complementos del 10.
Bonds Numbers o Números enlazados
Problemas gráficos y reales
Antes de comenzar los problemas escritos tras una exposición de hechos, es mejor comenzar con problemas reales, tanto en fotografía para que ellos, categoricen, extraigan datos, y observen lo que falta para realizar la pregunta y mostrar la solución.

Inicio al lenguaje matemático
Al representar siempre una igualdad o ecuación, siempre se puede representar en lenguaje matemático de forma sencilla. En el gráfico anterior se presentan
1+3=4 4-3=1 4-1=3
No solamente se trabaja cálculo.
Lectoescritura de números
Para la mejora del aprendizaje del concepto de número hay que presentar diferentes fichas de trabajo para que relacionen el símbolo numérico con el valor, el color.
Hay que realizar diferentes tarjetas, o flashcard

FlashCard o Tarjetas de Números.
Lúdico, uso de juegos matemáticos.
Matemáticas en Primaria
Cálculo

El cálculo se basa en la relación del Total y sus Partes; y siempre con su representación gráfica, tanto como números bond o como rejilla. También para el cálculo se usa los complementos del 10. Y muchos ejercicios se basan en complementos del 10, que en infantil se puede denominar amigos del 10. Así en cualquier cuenta el razonamiento sería este: 8-7=8+(2+5)=15
Ayuda al cálculo mental, ya que se basa en ir agrupando decenas o centenas. También ayuda a la descomposición numérica.
Inicio al lenguaje matemático; en el ejercicio anterior se plantea diferentes formas de expresión numérica:
8+7=15 15-7=8 15-8=7 (8+2)+5=15
También se plantea de forma natural las ecuaciones; al basarte en el TOTAL = PARTE1 + PARTE2 se juego a resolver ecuaciones desde niño.
Cálculo: Se manipula todas las operaciones; sumar, restar, multiplicar, dividir, raíz cuadrada,…

- Cálculo con Regletas Cuisinaire
Lo más sorprendente del cálculo y los problemas es que la solución ya está presente y por tanto es todo más concreto. También evita errores.
Representación visual de las propiedades de los números reales. Pueden manipular las propiedades y utilizarlas para el cálculo
Propiedad Conmutativa -> 2+4=4+2 3×4=4×3

Propiedad Asociativa -> 2+(1+4) = 2+(1+4) (2×3)x4 = 2x(3×4)

Elemento Identidad de la Suma -> 3+0=3
Elemento Identidad de la Multiplicación-> 4×1=4
Inverso Aditivo-> 6+(-6) = 0
Inverso Multiplicativo 5 x 1/5 = 1
Propiedad Distributiva 3x(3+4) = 3×3 + 3×4

Conceptos numéricos
Al trabajar de forma manipulativa y concreta se puede trabajar conceptos doble, triples, mitad, más, menos, igual de forma lúdica.


Problemas reales o gráficos
Como en la anterior etapa hay que presentar problemas reales o gráficos, donde haya que clasificar, ordenar o cuantificar. Tras presentar el problema se puede preguntar por:
¿Cuántos hay?
¿Quién tiene más?
¿Cuántos más?
¿Cuántos menos?
¿Cuántos tienen todos?
¿Cuántos falta para tener como el primero?
¿Cuánto es el doble del primero?
Por tanto están realizando problemas. Los pueden representar con regletas. Se pueden presentar fotografías de la clase donde hay sillas vacías, para realizar dichas preguntas.

Atención a la diversidad.
Con esta metodología, la atención a la diversidad está asegurada, al hacerlo más concreto el alumnado tiene acceso a su contenido y lo puede manipular. También es más fácil adaptar la actividad, por ejemplo se pueden usar regletas, o no. Se puede representar la expresión numérica o no. Se puede realizar el cálculo mental o regletas o determinado algoritmo. Es independiente del cálculo, se puede utilizar el tradicional o ABN. Por tanto el alumnado se puede incorporar a esta metodología en cualquier curso; incluso si existe desplazamiento desde otro colegio donde no esté implantado no tendrá dificultad.
Representación de números
Ya se ha comentado como se pueden representar los números con regletas. Podemos representar los números naturales, enteros, pares, impares, primos…


Sistema Métrico
Longitud.
Ideal para el uso de regletas, ya que las regletas son medidas de 1cm o 2cm. Realmente están midiendo desde infantil y utilizando medidas. Se puede pedir que midan el libro, goma lápiz, o cualquier elemento que tengan cercano.

Superficie.
Al igual que la longitud se pueden realizar superficies y cálculos con las misma regletas. También se puede pedir que midan la superficie del cuaderno, libreta, calcular su perímetro.

y sobre todo Resolución Gráfica de Problemas
Como punto de partida, vimos la dificultad de establecer una secuenciación de los problemas y su dificultad. Así partimos de una clasificación de problemas de ofrecida en un curso de formación por José Mª de la Rosa Sánchez, y cuya clasificación de los autores, J. Luis Luceño Campos y Jaime Martínez Montero, así como el Equipo de Orientación y Psicopedagógica de Ponferrada. Más información sobre clasificación de problemas.
Al interpretar el problema no de una forma no lineal, y extraer los datos como variables. No importa el orden, y por tanto los tipos de problemas de simplifican. Buscamos relaciones y su representación gráfica.
Se trabaja la comprensión del problema analizando si los datos que nos ofrece el problema son de otros datos. Por ejemplo en el problema:
Compré 12 pasteles. He regalado 6 pasteles a mi hermana ¿Cuántos me quedan?
Los 6 pasteles no son nuevos, son de los 12 que tengo. Por tanto están relacionados y por tanto aparecen en lugar opuesto de la ecuación.
Veamos un ejemplo práctico:

Problemas gráficos y reales.
Desde infantil ya se inicia los problemas, y son intrínsecos al número. Pudiendo ser adquiridos desde edades muy tempranas.
Antes de presentar los problemas hay que presentar problemas gráficos para la interiorización de las PARTES y TOTAL. Lo ideal es que se inicia en forma de juegos o juegos educativos y al final con fotografía, o imágenes. Ejemplos: cartas, mecanos, dominó, pesas… Planteamos trabajar diariamente 10 minutos. Desde problemas verbales, problemas en imágenes, o resolución de problemas.
Resolución de Problemas
Problema de Cambio 1
Problemas de Cambio 2
Problemas de Cambio 3
Problemas de Combinación 1
Problemas de Combinación 2
Problemas de Cambio con Fracciones
Problemas de Multiplicación 1
Más ejemplos:
Elementos que componen la Resolución de Problemas
DATOS
Como metodología general es la separación y análisis de las variables o DATOS dentro del problema y detectar su relación. Así los datos se presenta no de una forma lineal sino relacional, facilitando su posterior representación.
Lo que se pretende es que las variables sean datos, y por tanto independiente del orden de escritura o lectura; favoreciendo la comprensión del problema, ya que favorece descubrir la relación entre datos.
Representación Gráfica
La solución gráfica, favorece la comprensión del problema, evita errores, y es el inicio del lenguaje matemático. Con estos problemas se pueden presentar la solución en forma de expresión.
9-5=?
5+?=9
9=5+?
No hay una solución, hay varias formas de resolver el problema.
Como se ha mencionado la solución se hace visible y evita frustración o usar el ensayo y error, muy común entre el alumnado.
Cálculo
El cálculo es independiente de la resolución del problema, es una parte que irá en relación de las competencias del alumnado. En un principio se realizarán cálculos manipulativos y concretos, para ir abstrayendo cada vez más, hasta llegar al uso de calculadora o uso de ordenador. La elección de un algoritmo depende del centro de del tutor/a, y siendo independiente de esta metodología. Como se ha mencionado nos basamos en la resolución del problema, no en el cálculo del mismo.
En alguna aulas hemos iniciado el algoritmo ABN, y en otras el alumnado utiliza el tradicional. Consideramos las ventajas del algoritmo ABN, pero primero resolviendo el problema de forma gráfica.
Prueba
Se puede comprobar las soluciones de los problemas sumando las PARTES, y tendrá que dar el TOTAL.
¿Cómo resolver un problema?
Como idea al alumnado se le ha mencionado que no es un problema sino que es un puzzle, así aumenta en nivel lúdico. No es lo mismo resolver un problema que resolver un puzzle.
1º Lectura con atención del problema.
2º Extracción de datos convirtiéndolos en DATOS y regletas.
3º Buscar relaciones de los datos, facilitará la realización del gráfico.
4º Realización de la solución gráfica.
5º Dependiendo del nivel, escribir la expresión numérica.
6º Cálculo
7º Realización de la prueba. Sumando PARTES.
Así se plantea un esquema para la realización de problemas.
Tipos de Problemas
La solución gráfica dependerá del tipo de problemas y nuestra clasificación es:
Problemas de Cambio
Las diferentes expresiones numéricas serían
x + y = z
x – y = z
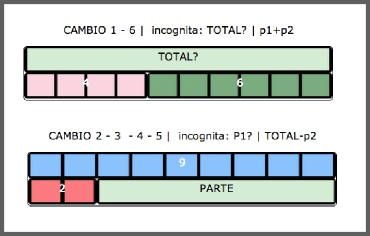
Problemas de Combinación
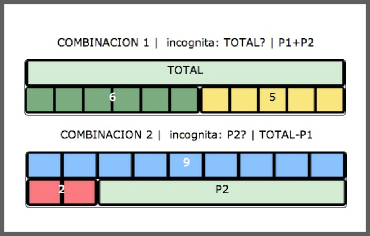
Problemas de Comparación
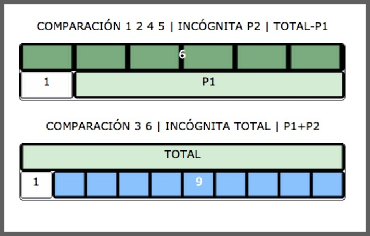
Problemas de Igualación
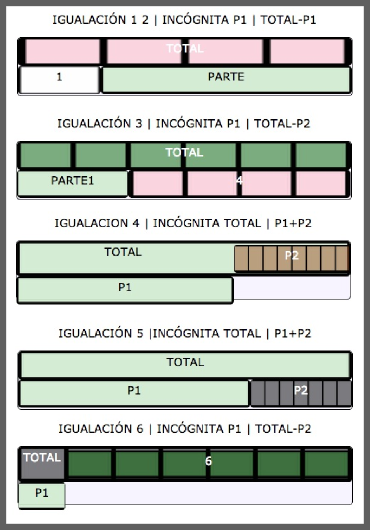
Problemas de Multiplicación
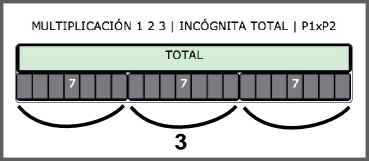
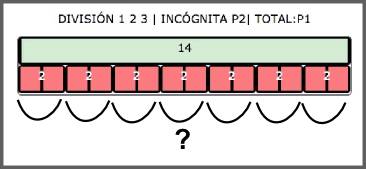
Problemas de División
Problemas complejos.
Hemos visto los tipos de problemas, según sus variables y sus relaciones con la incógnita. Ahora hay que mencionar distintos tipos de problemas relacionados con distintos números. En este caso fracciones, porcentajes, ángulos, superficies.
Problemas con Fracciones
Realmente se realizan igual que si fuera una división. En el comienzo se pueden utilizar puntos, o las mismas regletas para repartir, para posteriormente utilizar los números.
Problemas con Porcentajes
La secuenciación del trabajo con porcentaje es comenzar por 50%, luego trabajar múltiplos del 10% luego múltiplos del 5% , 1%.
Todo se basa en el 10% que se puede calcular mentalmente. 10% de 20 = 2 20/10= 2

Problemas de ángulos.

Ángulos Adyacentes.

Sistema métrico
Se presentarán problemas de medidas.
Dinero
Se presentarán problemas de cálculo de dinero, si compran elementos o si falta o sobra.
Tiempo
Trabajar el tiempo es complejo ya que no se puede tocar y al percepción del tiempo es relativa.
Con varias operaciones.
Finalmente se trabajará problemas con más relaciones entre variables y unión de tipos de problemas.

Evaluación
Se ha cambiado la forma de trabajar del alumnado y por tanto la evaluación será diferente. Presentamos modelo de rúbrica para la evaluación.
Se ha realizado una rúbrica para la evaluación de la realización de Problemas.
Se basa en analizar distintas partes de la resolución de problemas según Singapore Math. Así analizamos la extracción y análisis de los datos, la representación gráfica, el cálculo (independiente del algoritmo), prueba, y claridad en la realización.
Creación e invención de problemas
Es fácil crear el ambiente necesario para que el alumnado cree su propios problemas y los resuelva. Es interesante la creación de problemas de forma oral. También la resolución gráfica solamente.

Tratamiento de la información
Con el uso de las regletas es fácil recopilar información y representarlas en gráficas.

Uso del lenguaje matemático
Todo el proceso llega al uso del lenguaje matemático, para facilitar el sistema de ecuaciones, resolución de problemas complejos e interpretación matemática de la realidad. Y como ejercicio final te retamos a que realices la expresión numérica de esta imagen.

Herramientas y Documentos.
Hemos creado varias herramientas para generar recursos basados en «Matemáticas basadas en la Resolución de Problemas«
Herramientas
Simetría.
Patrones.
Cuadrados Mágicos.
Jugar a patrones.
Pirámides Numéricas.
Problemas interactivos.
Imprimir Problemas.
Código Secreto
Documentos
También la creación de una colección de Actividades para descargar.
Conclusiones
Estamos en un tiempo de cambios, avances y hay que estar preparado para tomar las elecciones adecuadas. Creemos que en unos años se presentarán varios métodos, «Algoritmo ABN«, «Método Singapur«, Tradicional y habrá que elegir por uno de ellos. Nosotros presentamos uno ecléctico «Matemáticas basadas en la Resolución de Problemas» que conlleva el uso del lenguaje matemático de formar divertida. Y si has llegado hasta aquí te animo a que pruebes con tu alumnado, mis clases han cambiado, yo he cambiado, mis alumnos han cambiado.
Agradecimientos
Especial Agradecimientos al profesorado del CEIP Cristóbal Luque Onieva, de Priego de Córdoba; que desde hace varios años trabajamos con esta Metodología, que aún está viva y en crecimiento; Carlos Valero, Pepe Yepes, María José Vasco, Juan Francisco López Lombardo, Conchi Cuadros, Mari Carmen España, Mercedes, Rocio, Paco Pulido, Maribel, Lourdes, Manuela, Concha Jiménez, Alonso Arroyo y un servidor, Juan Carlos Sarmiento.
Nuestra comunidad. ¿Quieres participar?
¿quieres colaborar con la elaboración de materiales?
envía documentos a olesur@gmail.com
Asunto: materiales maetmáticas
(Autor, Colegio, Tipo de ejercicio, Licencia, Archivo en Jpg, pdf )
Estamos trabajando para enviarlos desde esta plataforma…
pero por ahora, con el envio tradicional de email.
Nos encontrarás en:
Facebook: https://www.facebook.com/metodosingapore
Pinterest: http://www.pinterest.com/olesur/m%C3%A9todo-singapore/
Twitter: https://twitter.com/metodosingapore
Aplicaciones Interactivas: olesur.com
Fichas para Imprimir: Recursos Educativos
© 2014 Juan Carlos Sarmiento Montoro
Maestro Pedagogía Terapéutica
CEIP Cristóbal Luque Onieva
Priego de Córdoba
olesur@gmail.com
+34630770928


 Ordenación
Ordenación








